Institute for Information and Communication Systems, Neural and Fuzzy Systems
Universitaetsplatz 2, D-39106 Magdeburg, Germany
Phone : +49.391.67.11358, Fax : +49.391.67.12018
Keywords: hybrid methods, neuro-fuzzy system, system control,
neural network, fuzzy system
Abstract
A first prototype of a fuzzy controller can be designed rapidly in most cases. The optimization process is usually more time consuming since the system must be tuned by 'trial-and-error' methods. To simplify the design and optimization process learning techniques derived from neural networks (so called neuro-fuzzy approaches) can be used. In this paper we describe an updated version of the neuro-fuzzy model NEFCON. This model is able to learn and to optimize the rulebase of a Mamdani-like fuzzy controller online by a reinforcement learning algorithm that uses a fuzzy error measure. Therefore we also describe some methods to determine a fuzzy error measure of a dynamic system. Besides we present an implementation of the model and an application example under the MATLAB/SIMULINK development environment. The optimized fuzzy controller can be detached from the development environment and can be used in realtime environments. The tool is available via the Internet.
The main problems in fuzzy controller design are the construction of an initial rulebase and in particular the optimization of an existing rulebase. The methods presented in this paper have been developed to support the user in both of these cases.
One of the main objectives of our project is to develop algorithms that are able to determine online an appropriate and interpretable rulebase within a small number of simulation runs. Besides it must be possible to use prior knowledge to initialize the learning process. This is a contrast to 'pure' reinforcement strategies [3] or methods based on dynamic programming [1; 15], which try to find an optimal solution using neural network structures. These methods need many runs to find even an approximate solution for a given control problem. On the other hand, they have the advantage that they need less information about the error of the current system state. However, in many cases a simple error description can be achieved with little effort. In this paper we present some methods to determine a fuzzy error measure of a dynamic system.
The first prototype implementation of the described algorithms and the development of a user friendly interface was done in cooperation with the Daimler-Benz Aerospace Airbus GmbH, Hamburg [14]. The tool can be obtained free of charge for non-commercial purposes from our Internet Web-Server (http://fuzzy.cs.uni-magdeburg.de/nefcon or ftp://fuzzy.cs.uni-magdeburg.de/pub/nefconma).
The NEFCON-Model is based on a generic fuzzy perceptron [9; 11;
12]. An example, which describes the
structure of a fuzzy controller with 5 rules, 2 inputs, and one output
is shown in Figure 1. The inner nodes R1,
... , R5 represent the rules, the nodes ![]() ,
,
![]() , and
, and ![]() the input and output values, and
the input and output values, and ![]() ,
,
![]() the fuzzy sets describing the
antecedents
the fuzzy sets describing the
antecedents ![]() and consequents
and consequents
![]() . Rules with the same antecedent
use so-called shared weights, which are represented by ellipses (see Figure 1).
They ensure the integrity of the rulebase. The node R1 for
example represents the rule:
. Rules with the same antecedent
use so-called shared weights, which are represented by ellipses (see Figure 1).
They ensure the integrity of the rulebase. The node R1 for
example represents the rule: ![]() .
.
Figure 1. A NEFCON System with two inputs, 5 rules and one output
The learning process of the NEFCON model can be divided into two main phases. The first phase is designed to learn an initial rulebase, if no prior knowledge about the system is available. Furthermore it can be used to complete a manually defined rulebase. The second phase optimizes the rules by shifting or modifying the fuzzy sets of the rules. Both phases use a fuzzy error E, which describes the quality of the current system state, to learn or to optimize the rulebase.
The fuzzy error plays the role of the critic element in reinforcement
learning models (e.g. [3; 2]).
In addition the sign of the optimal output value ![]() opt must be
known. So the extended fuzzy error E* is defined as
opt must be
known. So the extended fuzzy error E* is defined as
E*(x1, ..., xn) = sgn(![]() opt)
E(x1, ..., xn),
opt)
E(x1, ..., xn),
with the crisp input (x1, ..., xn).
The updated NEFCON learning algorithm learns and optimizes the rulebase of a Mamdani like fuzzy controller [8]. The fuzzy sets of the antecedents and consequents can be represented by any symmetric membership function. Triangular, trapezoidal, and Gaussian functions are supported by the presented implementation.
Methods to learn an initial rulebase can be divided into three classes: Methods starting with an empty rulebase [13; 17], methods starting with a 'full' rulebase (combination of every fuzzy set in the antecedents with every consequent) [10] and methods starting with a random rulebase [7]. We implemented algorithms of the first two classes.
The modified algorithm NEFCON I is based on the original NEFCON model
[10; 12]. It
starts with a 'full' rulebase. The algorithm can be divided into two phases
which are executed for a fixed period of time or a fixed number of iteration
steps. During the first phase, rules with an output sign different from
that of the optimal output value ![]() opt are removed. During the
second phase, a rulebase is constructed for each control action by selecting
randomly one rule from every group of rules with identical antecedents.
The error of each rule (the output error of the whole network weighted
by the activation of the individual rule) is accumulated. At the end of
the second phase from each group of rule nodes with identical antecedents
the rule with the least error value remains in the rulebase. All other
rule nodes are deleted. In addition, rules used very rarely are removed
from the rulebase. The original algorithm used
triangular membership functions, while the improved implementation also supports
trapezoidal and Gaussian membership functions. Besides, the algorithm was
enhanced for dynamic systems which need a static offset.
opt are removed. During the
second phase, a rulebase is constructed for each control action by selecting
randomly one rule from every group of rules with identical antecedents.
The error of each rule (the output error of the whole network weighted
by the activation of the individual rule) is accumulated. At the end of
the second phase from each group of rule nodes with identical antecedents
the rule with the least error value remains in the rulebase. All other
rule nodes are deleted. In addition, rules used very rarely are removed
from the rulebase. The original algorithm used
triangular membership functions, while the improved implementation also supports
trapezoidal and Gaussian membership functions. Besides, the algorithm was
enhanced for dynamic systems which need a static offset.
The 'Bottom-Up'-Algorithm starts with an empty rulebase. An initial fuzzy partitioning of the input and output intervals must be given. The algorithm can be divided into two phases. During the first phase, the rules' antecedents are determined by classifying the input values, i.e. finding that membership function for each variable that yields the highest membership value for the respective input value. Then the algorithm tries to 'guess' the output value by deriving it from the current fuzzy error. During the second phase the rulebase is optimized by changing the consequent to an adjacent membership function, if this is necessary. The improved implementation supports trapezoidal and Gaussian membership functions, too.
The 'Bottom-Up'-Algorithm is much faster than NEFCON I in case of a large number of input variables and a fine initial fuzzy partitioning. This is caused by the huge initial rulebase used by the NEFCON I algorithm. Nevertheless the 'Bottom-Up'-Algorithm should not be used for complex dynamic systems up to now, because of the heuristic approach of finding the consequents.
The algorithms presented in this section are designed to optimize a rulebase of a fuzzy controller by shifting and/or modifying the support of the fuzzy sets. They do not modify the rules or the structure of a given network.
The algorithm NEFCON I [12] is motivated
by the backpropagation algorithm for the multilayer perceptron. The extended
fuzzy error E* is used to optimize the rulebase by 'reward and
punishment'. A rule is 'rewarded' by shifting its consequent to a higher
value and by widening the support of the antecedents, if its current output
has the same sign as the optimal output ![]() opt. Otherwise the rule
is 'punished' by shifting its consequent to a lower value and by reducing
the support of the antecedents.
opt. Otherwise the rule
is 'punished' by shifting its consequent to a lower value and by reducing
the support of the antecedents.
The original model used monotonic membership functions [18] in the consequents to make it possible to use a backpropagation algorithm. In the current implementation this restriction was removed by storing the activation of every rule during the inference mechanism. Thus it is possible to use symmetric fuzzy sets in the consequents and the antecedents.
In contrast to the algorithm NEFCON I, which uses only the current fuzzy error E*, the algorithm NEFCON II also makes use of the change of the fuzzy error E* to optimize the rulebase [13]. This is a heuristic approach to include the dynamics of the system into the optimization process. Let E* be the extended fuzzy error at time t and E*' the extended fuzzy error at time t+1, then the error tendency is defined as
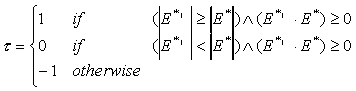
If = 0, the system moves to an optimal state. In this case the rulebase will not be modified. If = 1, the error is rising without changing its sign. The output of each rule is increased by shifting its consequents. The antecedents of rules with consequents increasing the output will be 'rewarded', while those with consequents decreasing the output will be 'punished'. If = -1, the system has overshot. The output is decreased and the antecedents 'punished' or 'rewarded' accordingly.
In case of a simple dynamic system the error can be described sufficiently well by simply using the difference between the reference signal and the system response. In case of more complex and sensitive systems the error must be described more exactly to obtain a satisfying rulebase with the presented algorithms.
The optimal state of a dynamic system can be described by a vector of system state variable values. Usually the state can not be described exactly, or we are content, if the system variables have roughly taken these values. Thus the quality of a current state can be described by fuzzy rules. With an error definition that uses a linguistic error description with fuzzy rules it is also easily possible to describe compensatory situations [12]. These are situations in which the dynamic system is driven towards its optimal state. In Figure 2 an error description is shown, which is part of the implementation. This rulebase also describes an overshoot situation (rules 7 and 8).
Figure 2. Sample Rulebase for Fuzzy Error Description
The error description with 'fuzzy intervals' has been developed for the presented implementation. It makes it possible to describe a 'soft' region for the system response which satisfies our request to the system behavior in a simple and intuitive way.
Figure 3 presents an error description for a simple switch signal. The error signal remains zero, if the response signal of the dynamic system stays in the defined interval between the reference signal and the bounds (thick lines). If the signal leaves the bounds of the interval, the fuzzy error is determined using a linguistic error definition as described above.
Figure 3. Sample of an Error Description using 'Fuzzy Intervals'
The aim of the implementation under MATLAB/SIMULINK was to develop an interactive tool for the construction and optimization of a fuzzy controller. This frees the user of programming and supports him to concentrate on controller design. It is possible to include prior knowledge into the system, to stop and to resume the learning process at any time, and to modify the rulebase and the optimization parameters interactively. Besides, a graphical user interface was designed to support the user during the development process of the fuzzy controller.
Figure 4 presents the simulation environment of a sample application during the optimization phase of the algorithm. The sample was created under Microsoft Windows NT 4.0.
Figure 4. Sample of a Development Environment under MATLAB/SIMULINK
(PT2 System)
As an example for the usability of the presented algorithms and error descriptions in practice, we present the simulation results concerning a conventional PT2 system. Simulation results concerning the classical inverted pendulum problem are comparable to the results obtained by the 'original' NEFCON algorithms presented in prior publications [10; 13; 12].
A PT2-system models the behavior of a two-mass system, for example a spring-damper combination or a revolution control for an electric motor (see [6; 16]). In classical control theory a PT2 system is controlled by a PI or a PID controller. A comparison to fuzzy controllers for this problem is considered e.g. in [4].
For the presented example we used a PT2 system that is given by the following differential equation:
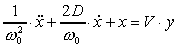 .
.
For the constants we chose 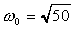 ,
,
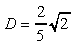 and
and 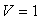 . The transfer
function of this system is defined as:
. The transfer
function of this system is defined as:
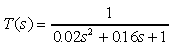 .
.
The reference signal y' and the fuzzy error
were described using 'fuzzy intervals' (see Figure 3). To control
the PT2 system a NEFCON system with one output signal
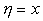 and three input signals (
and three input signals (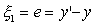 ,
,
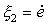 ,
, 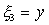 ) was used.
The algorithm NEFCON I was selected for the rule learning process,
since the heuristic approach of finding the conclusions used by
the algorithm NEFCON II would have resulted in an inappropriate
rulebase. The reason for this is the integral part, that is needed
for control (in a stable state (dy = 0) the dynamic system will
probably need an input value y != 0 to remain stable; e.g. an electric
motor needs an amperage unequal to zero to maintain a constant
number of revolutions). The algorithm NEFCON II was selected for
optimization. The input interval of each input variable was partitioned
by three trapezoidal fuzzy sets and the output interval by five
fuzzy sets. The simulation environment is shown in Figure 5.
) was used.
The algorithm NEFCON I was selected for the rule learning process,
since the heuristic approach of finding the conclusions used by
the algorithm NEFCON II would have resulted in an inappropriate
rulebase. The reason for this is the integral part, that is needed
for control (in a stable state (dy = 0) the dynamic system will
probably need an input value y != 0 to remain stable; e.g. an electric
motor needs an amperage unequal to zero to maintain a constant
number of revolutions). The algorithm NEFCON II was selected for
optimization. The input interval of each input variable was partitioned
by three trapezoidal fuzzy sets and the output interval by five
fuzzy sets. The simulation environment is shown in Figure 5.
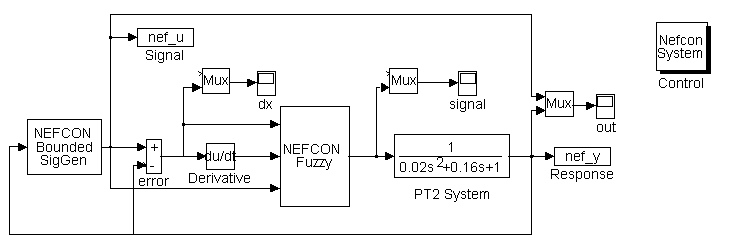
Figure 5. Simulation Environment for the PT2 System
The algorithm used a noisy reference signal during rule learning to improve the coverage of the system state space (see cycle 1-3 in Figure 8). The noise was produced by a signal generator included in the implementation. The learning algorithm was applied for 3 rule learning and 3 optimization cycles (with 167 iteration steps each cycle, where each cycle takes 5 seconds system time). The optimized rulebase consists of 25 rules (see Figure 7). The resulting fuzzy sets are shown in Figure 6.
After the learning process was finished, the controller was able to drive the system quite nicely along the desired course (see simulation cycle 7 in Figure 8). However, the control behavior is a little bit 'fidget'. This was implicitly tolerated by the error boundaries defined with the 'fuzzy intervals' and so it could not be improved during optimization.
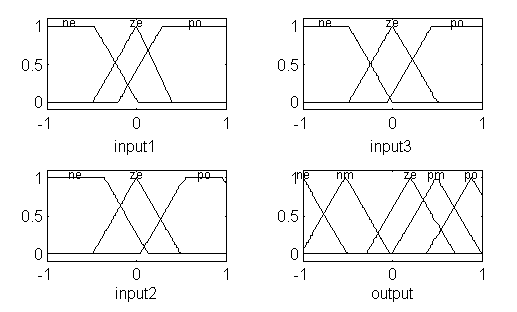
1. If (input1 is ne) and (input2 is ne) and (input3 is ne) then (output is ne) 2. If (input1 is ne) and (input2 is ne) and (input3 is ze) then (output is nm) 3. If (input1 is ne) and (input2 is ne) and (input3 is po) then (output is ne) 4. If (input1 is ne) and (input2 is ze) and (input3 is ne) then (output is ne) 5. If (input1 is ne) and (input2 is ze) and (input3 is ze) then (output is po) 6. If (input1 is ne) and (input2 is ze) and (input3 is po) then (output is nm) 7. If (input1 is ne) and (input2 is po) and (input3 is ne) then (output is nm) 8. If (input1 is ne) and (input2 is po) and (input3 is ze) then (output is nm) 9. If (input1 is ne) and (input2 is po) and (input3 is po) then (output is nm) 10. If (input1 is ze) and (input2 is ne) and (input3 is ne) then (output is po) 11. If (input1 is ze) and (input2 is ne) and (input3 is ze) then (output is nm) 12. If (input1 is ze) and (input2 is ne) and (input3 is po) then (output is ze) 13. If (input1 is ze) and (input2 is ze) and (input3 is ne) then (output is pm) 14. If (input1 is ze) and (input2 is ze) and (input3 is ze) then (output is ze) 15. If (input1 is ze) and (input2 is ze) and (input3 is po) then (output is pm) 16. If (input1 is ze) and (input2 is po) and (input3 is ne) then (output is pm) 17. If (input1 is ze) and (input2 is po) and (input3 is ze) then (output is po) 18. If (input1 is ze) and (input2 is po) and (input3 is po) then (output is po) 19. If (input1 is po) and (input2 is ne) and (input3 is ne) then (output is nm) 20. If (input1 is po) and (input2 is ne) and (input3 is ze) then (output is nm) 21. If (input1 is po) and (input2 is ne) and (input3 is po) then (output is ze) 22. If (input1 is po) and (input2 is ze) and (input3 is ze) then (output is ze) 23. If (input1 is po) and (input2 is ze) and (input3 is po) then (output is po) 24. If (input1 is po) and (input2 is po) and (input3 is ze) then (output is ze) 25. If (input1 is po) and (input2 is po) and (input3 is po) then (output is ze)
Figure 7. Learned Rulebase
Figure 8. Simulation Results for a PT2 System
By the implementation of the updated NEFCON model under MATLAB/SIMULINK it is possible to use the model conveniently for the design of fuzzy controllers for different dynamic systems. Additionally, the system configuration can be changed easily. The implementation was designed to be used as an interactive development tool.
In case of dynamic systems with little temporal dependence the rules of the controller will be learned and optimized within a small number of runs. The obtained fuzzy controller will be able to control the dynamic system appropriately. In addition the rulebase is always interpretable. In case of complex systems the quality of the results greatly depends on the definition of the error measure. This is caused by the fact that the NEFCON algorithms use only a simple approach to include the dynamics of the controlled system in the optimization process (see the credit assignment problem [3]). Some variations of reinforcement strategies [1; 7] have to be analyzed in order to determine if it is possible to integrate them into the optimization phase of the presented algorithms. It has to be checked whether they improve the quality of the controller without increasing the number of learning runs significantly.
Remark: MATLAB/SIMULINK is a simulation tool developed and distributed by 'The Mathworks' Inc., 24 Prime Park Way, Natick, Mass.01760; WWW: http://www.mathworks.com .
[1]![]() Barto, A.G.;
Bradtke, S. J.; Singh, S.
P.(1995): Learning to act using real-time dynamic programming, Artificial
Intelligence, Special Volume: Computational Research on Interaction and
Agency, 72(1): 81-138, 1995
Barto, A.G.;
Bradtke, S. J.; Singh, S.
P.(1995): Learning to act using real-time dynamic programming, Artificial
Intelligence, Special Volume: Computational Research on Interaction and
Agency, 72(1): 81-138, 1995
[2] Barto, A.G. (1992): Reinforcement Learning and Adaptive Critic Methods, In [17]
[3] Barto, A.G., Sutton R. S., Anderson, C. W. (1983): Neuronlike adaptive elements that can solve difficult learning control problems, IEEE Transactions on Systems, Man and Cybernetics, 13:834-846
[4] Knappe, Heiko (1994): Comparison of Conventional and Fuzzy-Control of Non-Linear Systems, in [5]
[5] Kruse, Rudolf; Gebhardt, Jörg; Palm, Rainer (Eds.) (1994): Fuzzy Systems in Computer Science, Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, Wiesbaden
[6] Leonhard, Werner (1992): Einführung in die Regelungstechnik, Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, Wiesbaden
[7] Lin, C.T. (1994): Neural Fuzzy Control Systems with structure and Parameter Learning, World Scientific Publishing, Singapore
[8] Mamdani, E. H.; Assilian S. (1973): An Experiment in Linguistic Synthesis with a Fuzzy Logic Controller, International Journal of Man-Machine Studies, 7:1-13
[9] ![]() Nauck, Detlef (1994):
A Fuzzy Perceptron as a Generic Model for Neuro-Fuzzy Approaches, In Proc.
of the 2nd German GI-Workshop Fuzzy-Systeme
'94, München
Nauck, Detlef (1994):
A Fuzzy Perceptron as a Generic Model for Neuro-Fuzzy Approaches, In Proc.
of the 2nd German GI-Workshop Fuzzy-Systeme
'94, München
[10] ![]() Nauck, Detlef and
Kruse, Rudolf (1993):
A Fuzzy Neural Network Learning Fuzzy Control Rules and Membership Functions
by Fuzzy Error Backpropagation, In Proc. IEEE
Int. Conf. on Neural Networks 1993, San Francisco
Nauck, Detlef and
Kruse, Rudolf (1993):
A Fuzzy Neural Network Learning Fuzzy Control Rules and Membership Functions
by Fuzzy Error Backpropagation, In Proc. IEEE
Int. Conf. on Neural Networks 1993, San Francisco
[11] Nauck, Detlef and Kruse, Rudolf (1996): Designing neuro-fuzzy systems through backpropagation, In Witold Pedryz, editor, Fuzzy Modelling: Paradigms and Practice, pages 203-228, Kluwer Academic Publishers, Boston, Dordrecht, London
[12] ![]() Nauck, Detlef; Klawonn,
Frank; Kruse, Rudolf
(1997): Foundations of Neuro-Fuzzy Systems, John Wiley & Sons, Inc., New York, Chichester, et.al.(to appear)
Nauck, Detlef; Klawonn,
Frank; Kruse, Rudolf
(1997): Foundations of Neuro-Fuzzy Systems, John Wiley & Sons, Inc., New York, Chichester, et.al.(to appear)
[13] ![]() Nauck, Detlef; Kruse,
Rudolf; Stellmach, Roland (1995): New Learning Algorithms for the Neuro-Fuzzy
Environment NEFCON-I, In Proceedings of Neuro-Fuzzy-Systeme '95, 357-364,
Darmstadt
Nauck, Detlef; Kruse,
Rudolf; Stellmach, Roland (1995): New Learning Algorithms for the Neuro-Fuzzy
Environment NEFCON-I, In Proceedings of Neuro-Fuzzy-Systeme '95, 357-364,
Darmstadt
[14] ![]() Nürnberger, Andreas
(1996): Entwurf und Implementierung des Neuro-Fuzzy-Modells NEFCON zur
Realisierung Neuronaler Fuzzy-Regler unter MATLAB/SIMULINK, Diplomarbeit,
Technische Universität Braunschweig
Nürnberger, Andreas
(1996): Entwurf und Implementierung des Neuro-Fuzzy-Modells NEFCON zur
Realisierung Neuronaler Fuzzy-Regler unter MATLAB/SIMULINK, Diplomarbeit,
Technische Universität Braunschweig
[15] ![]() Riedmiller, Martin;
Janusz, Barbara (1995):
Using Neural Reinforcement Controllers in Robotics, In Xian Yao, editor,
Proceedings of the 8th. Australian Conference on Artificial Intelligence,
Singapore, 1995, World Scientific Publishing,
Singapore
Riedmiller, Martin;
Janusz, Barbara (1995):
Using Neural Reinforcement Controllers in Robotics, In Xian Yao, editor,
Proceedings of the 8th. Australian Conference on Artificial Intelligence,
Singapore, 1995, World Scientific Publishing,
Singapore
[16] Tou, J. T. (1964): Modern Control Theory, McGraw Hill, New York
[17] Tschichold-Gürman, Nadine (1995): RuleNet - A new Knowledge-based Artificial Neural Network Model with Application Examples in Robotics, Dissertational Thesis, ETH Zürich
[18] Tsukamoto, Y. (1979): An Approach to Fuzzy Reasoning Method, In M. Gupta, R. Ragade and R. Yager, Hrsg.: Advances in Fuzzy Set Theory, North-Holland, Amsterdam
[19] ![]() White, D. A., Sofge, D. A., Publ. (1992): Handbook of Intelligent Control.
Neural, Fuzzy and Adaptive Approaches, Van Nostrand Reinhold, New York
White, D. A., Sofge, D. A., Publ. (1992): Handbook of Intelligent Control.
Neural, Fuzzy and Adaptive Approaches, Van Nostrand Reinhold, New York